Neural Networks

Perceptron

• single unit that takes in a set of input nodes, multiplies those inputs by weights, and adds a bias node, returning an output of 1 or 0
• perceptron visualization:

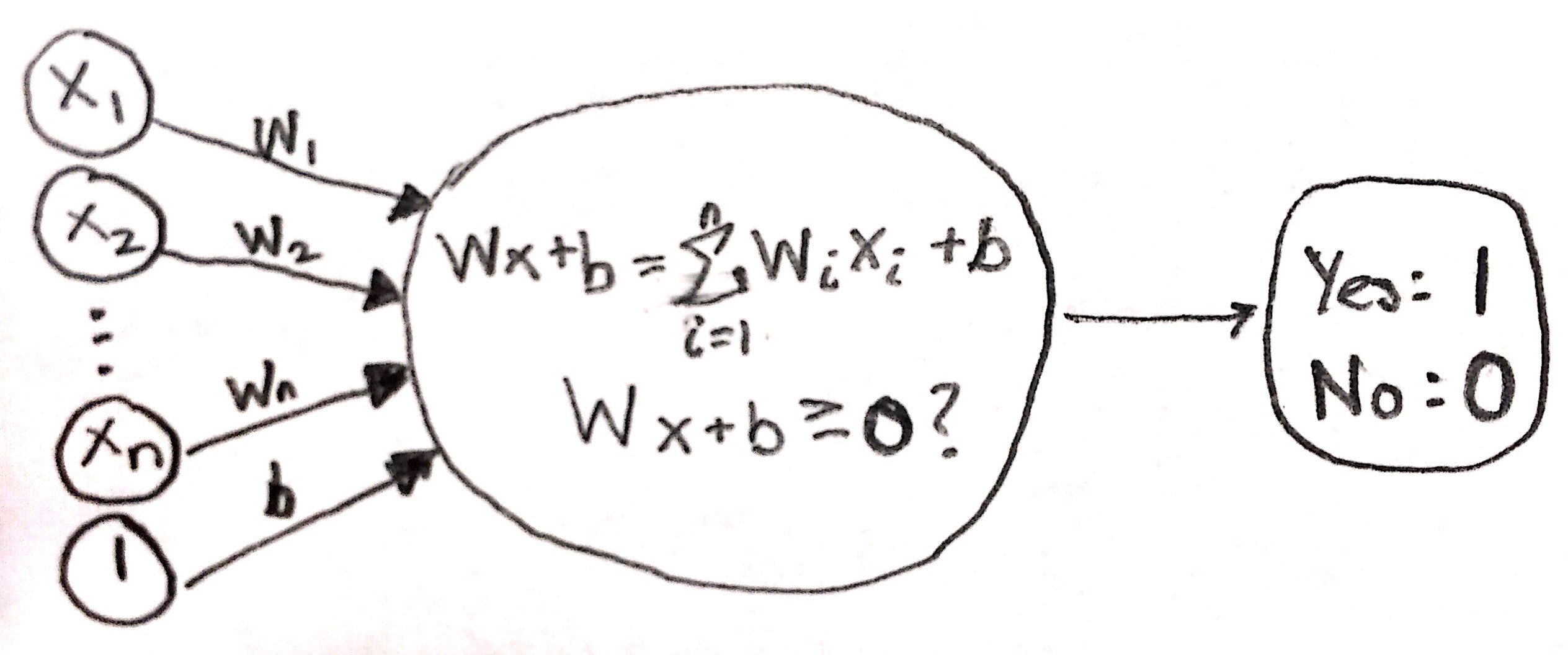
Perceptron Algorithm

• For all points \((p,q) \text{ with label } y\):
  • Calculate \(\hat{y} = step(w_{1} \cdot x_{1} + w_{2} \cdot x_{2} + b)\)
  • If the point is correctly classified: do nothing
  • If the point is classified positive, but it has a negative label: \(w_{1} - \alpha \cdot p\), \(w_{2} - \alpha \cdot q\), \(b - \alpha\)
  • If the point is classified negative, but it has a positive label: \(w_{1} + \alpha \cdot p\), \(w_{2} + \alpha \cdot q\), \(b + \alpha\)
  • (Where \(\alpha =\) learning rate)

Error Function

• measures the model’s performance
• must be continuous, not discrete, there should always be a direction towards a more optimal error

Importance of Activation Functions

• add non-linearity to a neural network, or else the entire neural network could be represented more simply by a single linear neuron
• squashes unbounded linear outputs from neuron so they do not explode

Sigmoid Activation Function

• sigmoid graph and equation:
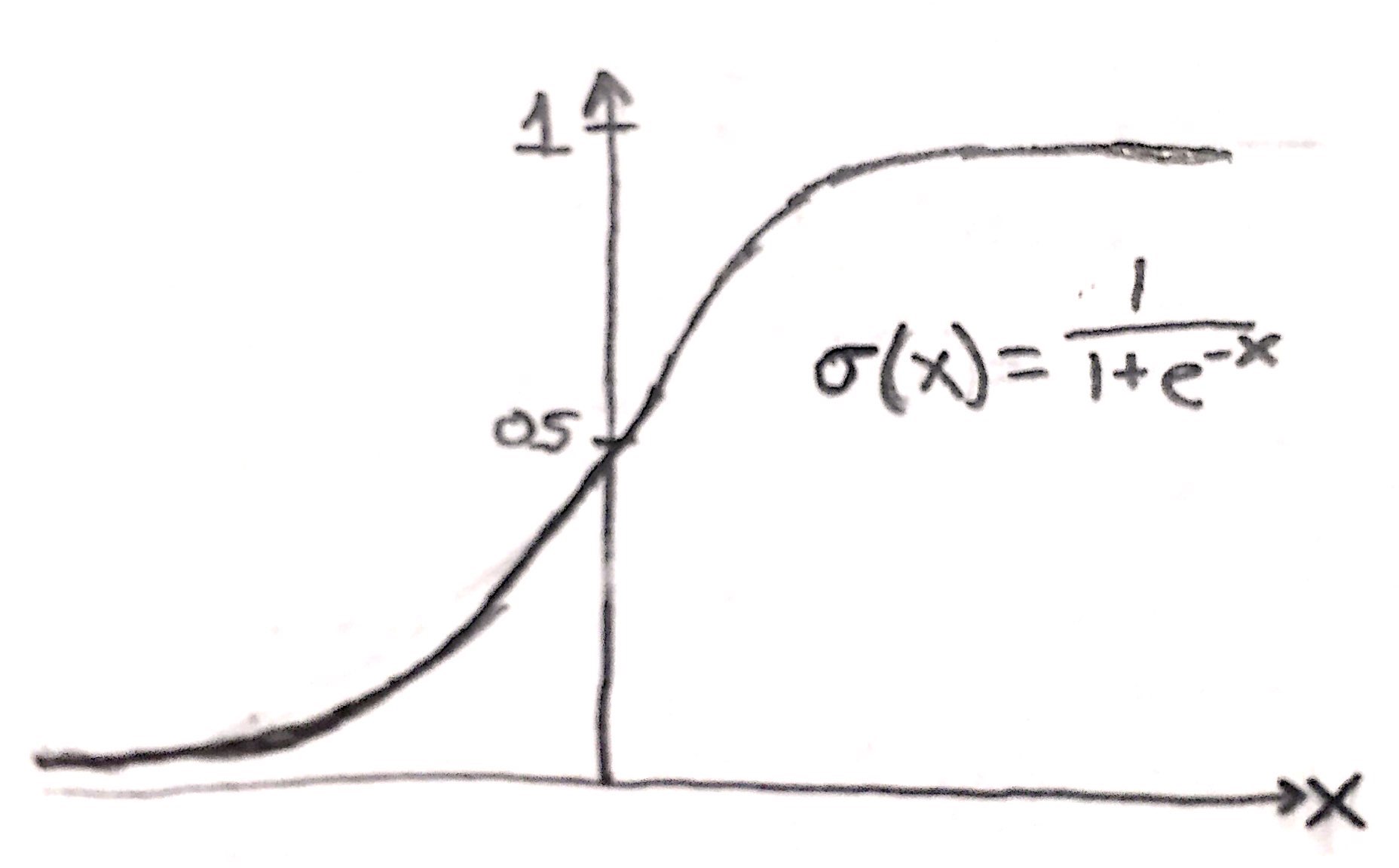
• takes in all real numbers and outputs a probability between 0 and 1
• allows a continuous error function

Softmax Function

• allows you to take linear set of scores for multiple classes and generate probabilities for each class that sum to 0
• exponent function used to avoid negative values (which can cause division by 0 if allowed)
• softmax equation:
  • Linear output of scores for \(n\) classes: \(Z_{1},Z_{2},\ldots,Z_{n}\)
  • \[P(\text{class } i) = \frac{e^{Z_{i}}}{e^{Z_{1}}+e^{Z_{2}}+\ldots+e^{Z_{n}}}\]
• softmax with 2 classes: \(n=2 \implies softmax(x)=sigmoid(x)\)

One-Hot Encoding

• with data that has multiple classes, assign a vector to each class (such that there is a 1 in the row that corresponds to the presence of the class, and the rest are all 0s)

Maximum Likelihood

• method of picking the model that gives the existing labels the highest probability
• how likely a model’s predictions are correct = product of the probabilities that every point is its labeled class
• maximizing the product of probabilities = best model

Cross-Entropy Error Function

Cross-Entropy Motivation

• maximum likelihood is able to measure a model’s performance
• products = hard to compute and yield small numbers (instead use sums = easy to calculate)
• use logs, because of the property \(log(ab) = log(a) + log(b)\) (allows our products to turn into sums)
• log(number_between_0_and_1) = negative numbers (instead use -log() = positive)
• if we use -log(), minimizing -log() = best model (because before, larger product = better model, and log(large_product) = small number, so now we need to minimize)

Cross-Entropy Notation

• \(m\) : number of training samples
• \(X_{i}\) : a specific train sample \(i\)
• \(n\) : number of features
• \(w_{j}\) : a specific feature weight
• \(x_{j}\) : a specific input feature
• \(\hat{y}_{i}\) : prediction for a specific train sample \(i\)

Cross-Entropy Equations

• Calculate predictions:

\[\begin{align}\hat{y}_{i}&=\sigma(WX_{i}+b) \\ \hat{y}_{i}&=\sigma(\sum_{j=1}^{n}w_{j}x_{j}+b) \\ \hat{y}_{i}&=\sigma(w_{1}x_{1}+\ldots+w_{n}x_{n}+b)\end{align}\]

• Cross Entropy (2 classes):

\[E=-\frac{1}{m}\sum_{i=1}^{m}y_{i}\ln(\hat{y}_{i})+(1-y_{i})\ln(1-\hat{y}_{i})\]

• Cross Entropy (2 classes, with W = weights, b = bias):

\[E(W,b)=-\frac{1}{m}\sum_{i=1}^{m}y_{i}\ln(\sigma(WX_{i}+b))+(1-y_{i})\ln(1-\sigma(WX_{i}+b))\]

• Cross Entropy (n classes):

\[E=-\sum_{i=1}^{m}\sum_{j=1}^{n}y_{ij}\ln(\hat{y}_{ij})\]

Cross-Entropy Explanations

• y = 1 or 0, therefore only one term in the summation is chosen, and that term will calculate the ln() of the correct probability, then sum the negative ln’s
• only take -ln() of probabilities that matter, formula when n = 2 turns out to be cross entropy formula for 2 classes

Gradient Descent

Gradient Descent Motivation

• we want to minimize the cross-entropy error to find the best model
• we need to find the lowest valley in the graph of error function and weights as that is where the error is least
• by taking negative partial derivative of error function with respect to each weight that is the direction to move in towards a lower error and a better model
• therefore we simply need to calculate the gradient of the error
• also gradient = scalar x coordinates of point (scalar = label - prediction), this means label close to the prediction = small gradient

Gradient Descent Notation

• \((x_{1},\ldots,x_{n})\) : features for a specific training sample
• \(X\) : vector of features
• \(X_{1},X_{2},\ldots,X_{m}\) : features vectors for \(m\) training samples
• \(y\) : label for training samples
• \(\hat{y}\) : predictions from algorithm for training samples
• \(E\) : cross entropy error
• \(\nabla E\) : gradient of error
• \((w_{1},\ldots,w_{n})\) : weights of algorithm
• \(\sigma(x)\) : sigmoid function
• \(\text{subscript}\ \ i\) : for specific training sample

GD Single Train Sample \(\nabla E_{i}\)

For a single training sample, \(X_{i}\):

\[\begin{align}\nabla E_{i} &= (\frac{\partial}{\partial w_{1}}E_{i},\ldots,\frac{\partial}{\partial w_{n}}E_{i},\frac{\partial}{\partial b}E_{i})\\ &= (\hat{y}_{i}-y_{i})(x_{1},\ldots,x_{n},1)\end{align}\]

Proof.

\[\text{Individual training sample predictions:}\\ \hat{y}_{i}=\sigma(WX_{i}+b)\] \[\text{Individual training sample error:}\\ E_{i}=-y_{i}\ln(\hat{y}_{i})-(1-y_{i})\ln(1-\hat{y}_{i})\] \[\text{Gradient is equal to partial derivatives of error for each weight:}\\ \nabla E_{i} = (\frac{\partial}{\partial w_{1}}E_{i},\ldots,\frac{\partial}{\partial w_{n}}E_{i},\frac{\partial}{\partial b}E_{i})\\\\\] \[\text{Sigmoid function derivative:}\\ \begin{align} \sigma'(x) &=\frac{d}{dx}\left(\frac{1}{1+e^{-x}}\right) \\ &=\frac{e^{-x}}{(1+e^{-x})^{2}} &&\text{(quotient rule)} \\ &=\frac{1}{1+e^{-x}}\cdot \frac{e^{-x}}{1+e^{-x}} \\ &=\sigma(x)(1-\sigma(x))&&\text{(long division)}\\\\ \end{align}\] \[\text{Partial derivative of prediction:}\] \[\begin{align} \frac{\partial}{\partial w_{j}}\hat{y}_{i}&=\frac{\partial}{\partial w_{j}}(\sigma(WX_{i}+b)) &&(\hat{y}_{i}\text{ formula)} \\ &= \sigma(WX_{i}+b)(1-\sigma(WX_{i}+b))\cdot\frac{\partial}{\partial w_{j}}(WX_{i}+b) &&(\sigma'(x) \text{ formula)}\\ &= \hat{y}_{i}(1-\hat{y}_{i})\cdot\frac{\partial}{\partial w_{j}}(WX_{i}+b) \\ &= \hat{y}_{i}(1-\hat{y}_{i})\cdot\frac{\partial}{\partial w_{j}}(w_{1}x_{1}+\ldots+w_{j}x_{j}+\ldots+w_{n}x_{n}+b) \\ &= \hat{y}_{i}(1-\hat{y}_{i})\cdot(0+\ldots+x_{j}+\ldots+0) &&\text{(partial derivative)}\\ &= \hat{y}_{i}(1-\hat{y}_{i})\cdot x_{j}\\\\ \end{align}\] \[\text{Partial derivative of error:}\] \[\begin{align}\frac{\partial}{\partial w_{j}}E_{i}&=\frac{\partial}{\partial w_{j}}(-y_{i}\ln(\hat{y}_{i})-(1-y_{i})\ln(1-\hat{y}_{i})) &&(E_{i}\text{ formula)}\\ &= -y_{i}(\frac{\partial}{\partial w_{j}}(\ln(\hat{y}_{i})))-(1-y_{i})(\frac{\partial}{\partial w_{j}}(\ln(1-\hat{y}_{i})))\\ &= -y_{i}(\frac{1}{\hat{y}_{i}}\cdot\frac{\partial}{\partial w_{j}}(\hat{y}_{i}))-(1-y_{i})(\frac{1}{1-\hat{y}_{i}}\cdot\frac{\partial}{\partial w_{j}}(1-\hat{y}_{i})) &&\text{(chain rule)}\\ &= -y_{i}(\frac{1}{\hat{y}_{i}}\cdot\hat{y}_{i}(1-\hat{y}_{i})x_{j})-(1-y_{i})(\frac{1}{1-\hat{y}_{i}}\cdot(-1)\hat{y}_{i}(1-\hat{y}_{i})x_{j})&&(\frac{\partial}{\partial w_{j}}\hat{y}_{i}\text{ formula)}\\ &= -y_{i}(1-\hat{y}_{i})x_{j}+(1-y_{i})\hat{y}_{i}\cdot x_{j}\\ &= (-y_{i}+y_{i}\hat{y}_{i}+\hat{y}_{i}-y_{i}\hat{y}_{i})x_{j}\\ &= -(y_{i}-\hat{y}_{i})x_{j}\\\\ \end{align}\] \[\text{By a similar proof:}\] \[\frac{\partial}{\partial b}E_{i}=-(y_{i}-\hat{y}_{i})\\\\\] \[\text{Gradient of error:}\] \[\begin{align} \nabla E_{i} &= (\frac{\partial}{\partial w_{1}}E_{i},\ldots,\frac{\partial}{\partial w_{n}}E_{i},\frac{\partial}{\partial b}E_{i})\\ &= \left(-(y_{i}-\hat{y}_{i})x_{1},\ldots,-(y_{i}-\hat{y}_{i})x_{n},-(y_{i}-\hat{y}_{i})\right)\\ &= -(y_{i}-\hat{y}_{i})(x_{1},\ldots,x_{n},1)\\ &= (\hat{y}_{i}-y_{i})(x_{1},\ldots,x_{n},1)\ \ \ \ \blacksquare\\\\ \end{align}\]

GD Overall \(\nabla E\)

For \(m\) training samples:

\[\nabla E = \frac{1}{m}\sum_{i=1}^{m}(\hat{y}_{i}-y_{i})(x_{1},\ldots,x_{n},1)\]

Proof.

\[\text{Overall error = average of individual train sample errors:}\] \[E=\frac{1}{m}\sum_{i=1}^{m}E_{i}\] \[\text{Overall gradient of error = average of individual train sample gradients:}\] \[\begin{align}\nabla E &= \frac{1}{m}\sum_{i=1}^{m}\nabla E_{i}\\ &=\frac{1}{m}\sum_{i=1}^{m}(\hat{y}_{i}-y_{i})(x_{1},\ldots,x_{n},1)\ \ \ \ \blacksquare\\\\\end{align}\]

Logistic Regression Algorithm

When Batch Size \(=1\)

1. Initialize random weights: \(w_{1},\ldots,w_{n},b\)
2. For every train sample: \(X_{1},\ldots,X_{m}\)
   • Update weights: \(w_{j}\leftarrow w_{j}-\alpha\frac{\partial}{\partial w_{j}}E_{i}\)
   • Update bias: \(b\leftarrow b-\alpha\frac{\partial}{\partial b}E_{i}\)
3. Repeat until error is small

When Batch Size \(=m\)

1. Initialize random weights: \(w_{1},\ldots,w_{n},b\)
2. For every batch:
   • Update weights:\(w_{j}\leftarrow w_{j}-\alpha\frac{1}{m}\sum_{i=1}^{m}\frac{\partial}{\partial w_{j}}E_{i}\)
   • Update bias:\(b\leftarrow b-\alpha\frac{1}{m}\sum_{i=1}^{m}\frac{\partial}{\partial b}E_{i}\)
3. Repeat until error is small

Neural Networks

• Built using Multi-Layer Perceptrons: essentially many layers of perceptrons feeding into one another such that each successive perceptron multiplies it’s input perceptrons by a learned weight
• Allows us to obtain non-linear models from linear models
• Deep Neural Network: has many layers of neurons
• Multi-Class Classification: apply softmax to the scores of multiple output perceptrons (bounds sum of probabilities for each class between 0 and 1)

NN Notation

• \(m\) : number of training samples
• \((x_{1},\ldots,x_{n})\) : features for a specific training sample
• \(X\) : vector of features
• \(X_{1},X_{2},\ldots,X_{m}\) : features vectors for \(m\) training samples
• \(y\) : label for training samples
• \(\hat{y}\) : predictions from algorithm for training samples
• \(E\) : cross entropy error
• \(\nabla E\) : gradient of error
• \(\sigma(x)\) : sigmoid function
• \(W^{(l)}_{ij}\) : weight of layer \(l\) that connects input neuron \(i\) to output neuron \(j\)
• \(W^{(l)}\) : weights vector for layer \(l\)
• \(s_{l}\) : number of neurons in layer \(l\)
• \(L\) : number of layers, including input layer
• \(z^{(l)}_{j}\) : the output of the \(j^{\text{th}}\) neuron in the \(l^{\text{th}}\) layer before applying sigmoid function
• \(a^{(l)}_{j}\) : the output of the \(j^{\text{th}}\) neuron in the \(l^{\text{th}}\) layer after applying sigmoid function
• \(\text{subscript}\ \ i\) : for specific training sample

NN Forward Propagation Equations

• Calculating NN predictions for train sample \(X_{i}\):

\[\hat{y}_{i}=\sigma(W^{(L-1)}(\sigma(W^{(L-2)}(\ldots(\sigma(W^{(1)}X_{i}))))))\]

• Example when \(L=4\):

\[\hat{y}_{i}=\sigma(W^{(3)}(\sigma(W^{(2)}(\sigma(W^{(1)}X_{i})))))\]

NN Backpropagation

Backprop Method Overview

• Perform Forward Propagation
• Calculate error
• Propagate error backwards (spread error to all weights)
• Update all weights using propagated error
• Loop until satisfied with error

Backprop Intuitive Understanding

• given a model’s error, propagate error backwards by decreasing the weights of neurons that had stronger connections over those that had weaker connections
• the error is caused more by those neurons with strong connections (or large weights), and decreasing their weights will reduce the effects of the erroneous neuron
• same as single perceptrons, calculate gradient of error function (which is more complex now) and use the gradient to update weights to descend to local minima

Why Understand Backprop?

• reference
• vanishing gradient problem: when error is back propagated through a NN, the gradient will decrease the further you move towards input layers (due to sigmoid activation function)
• must understand backpropagation intuition and math as if you do not, you can unintentionally stop NN training
• if you have sigmoid, relu, or any type of function that “cuts gradient flow”, like a hard thresholding of values (no matter if forward or backward propagation), then gradient will compute to 0 as taking derivative of something with 0 slope yields 0
• To Prevent Issues:
  • initialize weights properly
  • do not incorporate anything into NN that will “cut gradient flow” (the derivative of the thing yields 0 and that is being multiplied to calculate gradient)
  • check to make sure neurons are learning and gradients do not = 0

Sample NN Diagram

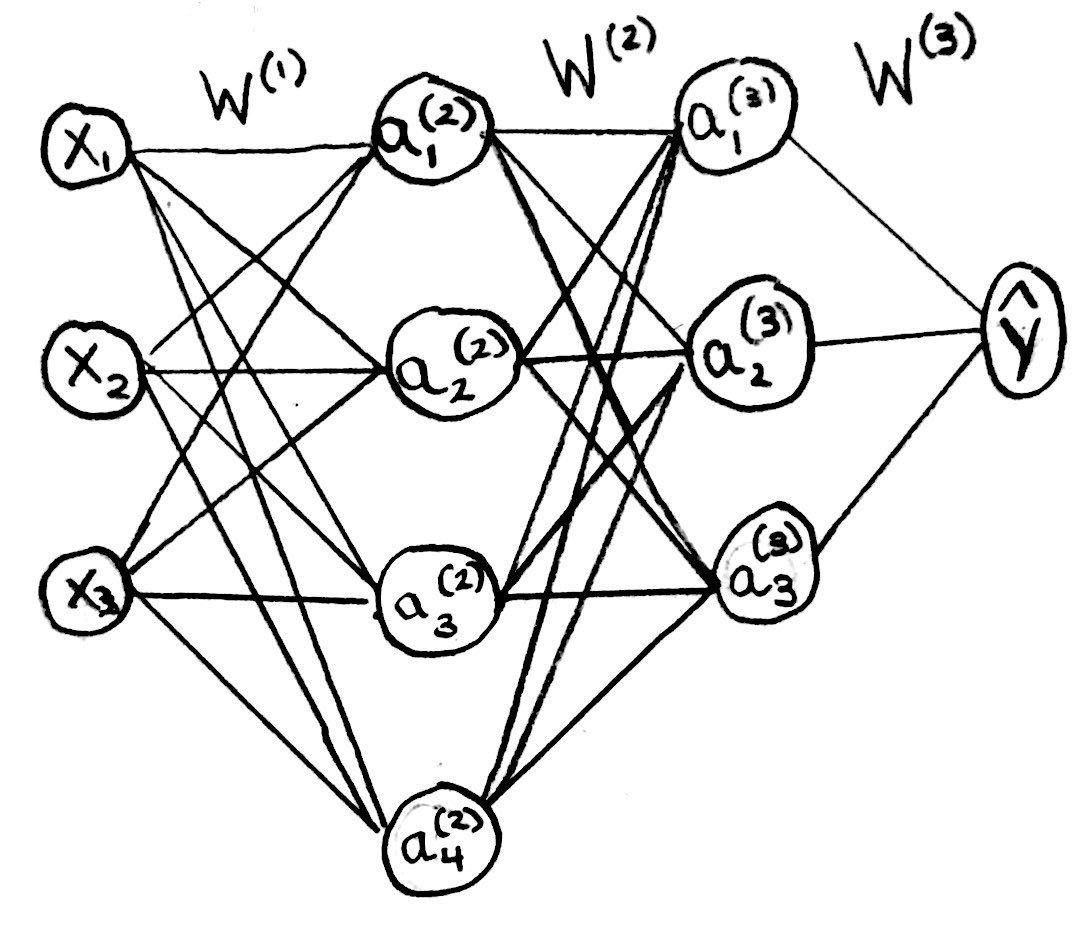
Calculating \(\frac{\partial}{\partial W^{(1)}_{11}}E\)

For the sample NN:

\[\begin{align} \frac{\partial}{\partial W^{(1)}_{11}}E &= \left(\frac{a_1^{(4)}-y}{a_1^{(4)}(1-a_1^{(4)})}\right) \\ &\phantom{0000} \cdot \left(a_1^{(4)}(1-a_1^{(4)})\right) \\ &\phantom{0000} \cdot \left(\left(W_{11}^{(3)} \cdot a_1^{(3)}(1-a_1^{(3)}) \cdot W_{11}^{(2)}\right) + \left(W_{21}^{(3)} \cdot a_2^{(3)}(1-a_2^{(3)}) \cdot W_{12}^{(2)}\right) + \left(W_{31}^{(3)} \cdot a_3^{(3)}(1-a_3^{(3)}) \cdot W_{13}^{(2)}\right)\right) \\ &\phantom{0000} \cdot \left(a_1^{(2)}(1-a_1^{(2)})\right) \\ &\phantom{0000} \cdot \left(a_1^{(1)}\right) \end{align}\]

Proof.

\[\text{For simplicity, Let:}\] \[\begin{align} x_1=a_1^{(1)},\ x_2&=a_2^{(1)},\ x_3=a_3^{(1)}, \\ \hat{y}&=a_1^{(4)} \end{align}\] \[\text{Equations from sample NN:}\] \[\begin{align} z_1^{(2)} &= W_{11}^{(1)}a_1^{(1)} + W_{21}^{(1)}a_2^{(1)} + W_{31}^{(1)}a_3^{(1)} \\ a_1^{(2)} &= \sigma(z_1^{(2)}) \\ z_1^{(3)} &= W_{11}^{(2)}a_1^{(2)} + W_{21}^{(2)}a_2^{(2)} + W_{31}^{(2)}a_3^{(2)} + W_{41}^{(2)}a_4^{(2)}\\ a_1^{(3)} &= \sigma(z_1^{(3)}) \\ z_2^{(3)} &= W_{12}^{(2)}a_1^{(2)} + W_{22}^{(2)}a_2^{(2)} + W_{32}^{(2)}a_3^{(2)} + W_{42}^{(2)}a_4^{(2)}\\ a_2^{(3)} &= \sigma(z_2^{(3)}) \\ z_3^{(3)} &= W_{13}^{(2)}a_1^{(2)} + W_{23}^{(2)}a_2^{(2)} + W_{33}^{(2)}a_3^{(2)} + W_{43}^{(2)}a_4^{(2)}\\ a_3^{(3)} &= \sigma(z_3^{(3)}) \\ z_1^{(4)} &= W_{11}^{(3)}a_1^{(3)} + W_{21}^{(3)}a_2^{(3)} + W_{31}^{(3)}a_3^{(3)} \\ a_1^{(4)} &= \sigma(z_1^{(4)}) \\ E &= -y\ln(a_1^{(4)})-(1-y)\ln(1-a_1^{(4)})\\\\ \end{align}\] \[\text{Recall chain rule:}\] \[\frac{\partial C}{\partial x} = \frac{\partial A}{\partial x} \cdot \frac{\partial B}{\partial A} \cdot \frac{\partial C}{\partial B}\\\\\] \[\text{The following is incorrect use of chain rule:}\] \[\frac{\partial E}{\partial W_{11}^{(1)}} = \frac{\partial E}{\partial a_1^{(4)}} \cdot \frac{\partial a_1^{(4)}}{\partial z_1^{(4)}} \cdot \frac{\partial z_1^{(4)}}{\partial a_1^{(3)}} \cdot \frac{\partial a_1^{(3)}}{\partial z_1^{(3)}} \cdot \frac{\partial z_1^{(3)}}{\partial a_1^{(2)}} \cdot \frac{\partial a_1^{(2)}}{\partial z_1^{(2)}} \cdot \frac{\partial z_1^{(2)}}{\partial W_{11}^{(1)}} \\\\\] \[\begin{align} \text{Incorrect because it only propagates error from }& a_1^{(4)}\to a_1^{(3)}\to a_1^{(2)}\to W_{11}^{(1)} \\ \text{And neglects error that also propagates from }& a_1^{(4)}\to a_2^{(3)}\to a_1^{(2)}\to W_{11}^{(1)} \\ \text{as well as from }& a_1^{(4)}\to a_3^{(3)}\to a_1^{(2)}\to W_{11}^{(1)} \\\\ \end{align}\] \[\text{Correct use of chain rule:}\] \[\frac{\partial E}{\partial W_{11}^{(1)}} = \frac{\partial E}{\partial a_1^{(4)}} \cdot \frac{\partial a_1^{(4)}}{\partial z_1^{(4)}} \cdot \frac{\partial z_1^{(4)}}{\partial a_1^{(2)}} \cdot \frac{\partial a_1^{(2)}}{\partial z_1^{(2)}} \cdot \frac{\partial z_1^{(2)}}{\partial W_{11}^{(1)}} \\\\\] \[\text{Calculating partial derivatives:}\] \[\begin{align} \frac{\partial E}{\partial a_1^{(4)}}&=\frac{\partial}{\partial a_1^{(4)}}(-y\ln(a_1^{(4)})-(1-y)\ln(1-a_1^{(4)}))\\ &=-y\cdot\frac{\partial}{\partial a_1^{(4)}}(\ln(a_1^{(4)})-(1-y)\cdot\frac{\partial}{\partial a_1^{(4)}}(\ln(1-a_1^{(4)}))\\ &=-y\cdot\frac{1}{a_1^{(4)}}\cdot 1-(1-y)\cdot\frac{1}{1- a_1^{(4)}}\cdot -1\\ &=\frac{a_1^{(4)}-y}{a_1^{(4)}(1-a_1^{(4)})} \\\\ \end{align}\] \[\begin{align} \frac{\partial a_1^{(4)}}{\partial z_1^{(4)}} &= \frac{\partial }{\partial z_1^{(4)}}(\sigma(z_1^{(4)})) \\ &= \sigma(z_1^{(4)})(1-\sigma(z_1^{(4)})) &&(\sigma'(x)=\sigma(x)(1-\sigma(x)) \\ &= a_1^{(4)}(1-a_1^{(4)}) &&(a_1^{(4)}=\sigma(z_1^{(4)})) \\\\ \end{align}\] \[\begin{align} \frac{\partial z_1^{(4)}}{\partial a_1^{(2)}} &= \frac{\partial }{\partial a_1^{(2)}}(W_{11}^{(3)}a_1^{(3)} + W_{21}^{(3)}a_2^{(3)} + W_{31}^{(3)}a_3^{(3)}) \\ &= \frac{\partial }{\partial a_1^{(2)}}(W_{11}^{(3)}\sigma(z_1^{(3)}) + W_{21}^{(3)}\sigma(z_2^{(3)}) + W_{31}^{(3)}\sigma(z_3^{(3)})) \\ &= W_{11}^{(3)} \cdot \frac{\partial }{\partial a_1^{(2)}}(\sigma(z_1^{(3)})) + W_{21}^{(3)} \cdot \frac{\partial }{\partial a_1^{(2)}}(\sigma(z_2^{(3)})) + W_{31}^{(3)} \cdot \frac{\partial }{\partial a_1^{(2)}}(\sigma(z_3^{(3)})) \\ &= W_{11}^{(3)} \cdot \sigma(z_1^{(3)})(1-\sigma(z_1^{(3)})) \cdot \frac{\partial }{\partial a_1^{(2)}}(z_1^{(3)}) \\ &\phantom{0000} + W_{21}^{(3)} \cdot \sigma(z_2^{(3)})(1-\sigma(z_2^{(3)})) \cdot \frac{\partial }{\partial a_1^{(2)}}(z_2^{(3)}) \\ &\phantom{0000} + W_{31}^{(3)} \cdot \sigma(z_3^{(3)})(1-\sigma(z_3^{(3)})) \cdot \frac{\partial }{\partial a_1^{(2)}}(z_3^{(3)}) \\ &= W_{11}^{(3)} \cdot a_1^{(3)}(1-a_1^{(3)}) \cdot \frac{\partial }{\partial a_1^{(2)}}(z_1^{(3)}) \\ &\phantom{0000} + W_{21}^{(3)} \cdot a_2^{(3)}(1-a_2^{(3)}) \cdot \frac{\partial }{\partial a_1^{(2)}}(z_2^{(3)}) \\ &\phantom{0000} + W_{31}^{(3)} \cdot a_3^{(3)}(1-a_3^{(3)}) \cdot \frac{\partial }{\partial a_1^{(2)}}(z_3^{(3)}) \\ &= W_{11}^{(3)} \cdot a_1^{(3)}(1-a_1^{(3)}) \cdot \frac{\partial }{\partial a_1^{(2)}}(W_{11}^{(2)}a_1^{(2)} + W_{21}^{(2)}a_2^{(2)} + W_{31}^{(2)}a_3^{(2)} + W_{41}^{(2)}a_4^{(2)}) \\ &\phantom{0000} + W_{21}^{(3)} \cdot a_2^{(3)}(1-a_2^{(3)}) \cdot \frac{\partial }{\partial a_1^{(2)}}(W_{12}^{(2)}a_1^{(2)} + W_{22}^{(2)}a_2^{(2)} + W_{32}^{(2)}a_3^{(2)} + W_{42}^{(2)}a_4^{(2)}) \\ &\phantom{0000} + W_{31}^{(3)} \cdot a_3^{(3)}(1-a_3^{(3)}) \cdot \frac{\partial }{\partial a_1^{(2)}}(W_{13}^{(2)}a_1^{(2)} + W_{23}^{(2)}a_2^{(2)} + W_{33}^{(2)}a_3^{(2)} + W_{43}^{(2)}a_4^{(2)}) \\ &= W_{11}^{(3)} \cdot a_1^{(3)}(1-a_1^{(3)}) \cdot \left(\frac{\partial }{\partial a_1^{(2)}}(W_{11}^{(2)}a_1^{(2)}) + 0 + 0 + 0 \right) \\ &\phantom{0000} + W_{21}^{(3)} \cdot a_2^{(3)}(1-a_2^{(3)}) \cdot \left(\frac{\partial }{\partial a_1^{(2)}}(W_{12}^{(2)}a_1^{(2)}) + 0 + 0 + 0 \right) \\ &\phantom{0000} + W_{31}^{(3)} \cdot a_3^{(3)}(1-a_3^{(3)}) \cdot \left(\frac{\partial }{\partial a_1^{(2)}}(W_{13}^{(2)}a_1^{(2)}) + 0 + 0 + 0 \right) \\ &= \left(W_{11}^{(3)} \cdot a_1^{(3)}(1-a_1^{(3)}) \cdot W_{11}^{(2)}\right) + \left(W_{21}^{(3)} \cdot a_2^{(3)}(1-a_2^{(3)}) \cdot W_{12}^{(2)}\right) + \left(W_{31}^{(3)} \cdot a_3^{(3)}(1-a_3^{(3)}) \cdot W_{13}^{(2)}\right) \\\\ \end{align}\] \[\begin{align} \frac{\partial a_1^{(2)}}{\partial z_1^{(2)}} &= \frac{\partial }{\partial z_1^{(2)}}(\sigma(z_1^{(2)})) \\ &= \sigma(z_1^{(2)})(1-\sigma(z_1^{(2)})) \\ &= a_1^{(2)}(1-a_1^{(2)}) \\\\ \end{align}\] \[\begin{align} \frac{\partial z_1^{(2)}}{\partial W_{11}^{(1)}} &= \frac{\partial }{\partial W_{11}^{(1)}}(W_{11}^{(1)}a_1^{(1)} + W_{21}^{(1)}a_2^{(1)} + W_{31}^{(1)}a_3^{(1)}) \\ &= \frac{\partial }{\partial W_{11}^{(1)}}(W_{11}^{(1)}a_1^{(1)}) + 0 + 0 \\ &= a_1^{(1)} \\\\ \end{align}\] \[\text{Using calculated partial derivatives and chain rule:}\] \[\begin{align} \frac{\partial E}{\partial W_{11}^{(1)}} &= \frac{\partial E}{\partial a_1^{(4)}} \cdot \frac{\partial a_1^{(4)}}{\partial z_1^{(4)}} \cdot \frac{\partial z_1^{(4)}}{\partial a_1^{(2)}} \cdot \frac{\partial a_1^{(2)}}{\partial z_1^{(2)}} \cdot \frac{\partial z_1^{(2)}}{\partial W_{11}^{(1)}} \\\\ &= \left(\frac{a_1^{(4)}-y}{a_1^{(4)}(1-a_1^{(4)})}\right) \\ &\phantom{0000} \cdot \left(a_1^{(4)}(1-a_1^{(4)})\right) \\ &\phantom{0000} \cdot \left(\left(W_{11}^{(3)} \cdot a_1^{(3)}(1-a_1^{(3)}) \cdot W_{11}^{(2)}\right) + \left(W_{21}^{(3)} \cdot a_2^{(3)}(1-a_2^{(3)}) \cdot W_{12}^{(2)}\right) + \left(W_{31}^{(3)} \cdot a_3^{(3)}(1-a_3^{(3)}) \cdot W_{13}^{(2)}\right)\right) \\ &\phantom{0000} \cdot \left(a_1^{(2)}(1-a_1^{(2)})\right) \\ &\phantom{0000} \cdot \left(a_1^{(1)}\right) \ \ \ \ \blacksquare\\\\ \end{align}\]

Calculating \(\frac{\partial}{\partial W^{(1)}_{21}}E\)

For the sample NN:

\[\begin{align} \frac{\partial}{\partial W^{(1)}_{21}}E &= \left(\frac{a_1^{(4)}-y}{a_1^{(4)}(1-a_1^{(4)})}\right) \\ &\phantom{0000} \cdot \left(a_1^{(4)}(1-a_1^{(4)})\right) \\ &\phantom{0000} \cdot \left(\left(W_{11}^{(3)} \cdot a_1^{(3)}(1-a_1^{(3)}) \cdot W_{11}^{(2)}\right) + \left(W_{21}^{(3)} \cdot a_2^{(3)}(1-a_2^{(3)}) \cdot W_{12}^{(2)}\right) + \left(W_{31}^{(3)} \cdot a_3^{(3)}(1-a_3^{(3)}) \cdot W_{13}^{(2)}\right)\right) \\ &\phantom{0000} \cdot \left(a_1^{(2)}(1-a_1^{(2)})\right) \\ &\phantom{0000} \cdot \left(a_2^{(1)}\right) \end{align}\]

Proof.

\[\text{Virtually identical proof as $\frac{\partial}{\partial W^{(1)}_{11}}E$,} \\ \text{Except for one partial derivative:}\] \[\frac{\partial E}{\partial W_{11}^{(1)}} = \frac{\partial E}{\partial a_1^{(4)}} \cdot \frac{\partial a_1^{(4)}}{\partial z_1^{(4)}} \cdot \frac{\partial z_1^{(4)}}{\partial a_1^{(2)}} \cdot \frac{\partial a_1^{(2)}}{\partial z_1^{(2)}} \cdot \frac{\partial z_1^{(2)}}{\partial W_{21}^{(1)}} \\\\\] \[\text{Calculating $\frac{\partial z_1^{(2)}}{\partial W_{21}^{(1)}}$:}\] \[\begin{align} \frac{\partial z_1^{(2)}}{\partial W_{21}^{(1)}} &= \frac{\partial }{\partial W_{21}^{(1)}}(W_{11}^{(1)}a_1^{(1)} + W_{21}^{(1)}a_2^{(1)} + W_{31}^{(1)}a_3^{(1)}) \\ &= 0 + \frac{\partial }{\partial W_{21}^{(1)}}(W_{21}^{(1)}a_2^{(1)}) + 0 \\ &= a_2^{(1)} \\\\ \end{align}\] \[\text{Reusing previously calculated partial derivatives,} \\ \text{and $\frac{\partial z_1^{(2)}}{\partial W_{21}^{(1)}}$, yields desired result} \ \ \ \ \blacksquare\\\\\]

Calculating \(\frac{\partial}{\partial W^{(3)}_{11}}E\)

For the sample NN:

\[\begin{align} \frac{\partial}{\partial W^{(3)}_{11}}E &= \left(\frac{a_1^{(4)}-y}{a_1^{(4)}(1-a_1^{(4)})}\right) \cdot \left(a_1^{(4)}(1-a_1^{(4)})\right) \cdot \left( a_1^{(3)}\right) \end{align}\]

Proof.

\[\text{For simplicity, Let:}\] \[\begin{align} x_1=a_1^{(1)},\ x_2&=a_2^{(1)},\ x_3=a_3^{(1)}, \\ \hat{y}&=a_1^{(4)} \end{align}\] \[\text{Equations from sample NN:}\] \[\begin{align} z_1^{(4)} &= W_{11}^{(3)}a_1^{(3)} + W_{21}^{(3)}a_2^{(3)} + W_{31}^{(3)}a_3^{(3)} \\ a_1^{(4)} &= \sigma(z_1^{(4)}) \\ E &= -y\ln(a_1^{(4)})-(1-y)\ln(1-a_1^{(4)})\\\\ \end{align}\] \[\text{Using chain rule:}\] \[\frac{\partial E}{\partial W_{11}^{(3)}} = \frac{\partial E}{\partial a_1^{(4)}} \cdot \frac{\partial a_1^{(4)}}{\partial z_1^{(4)}} \cdot \frac{\partial z_1^{(4)}}{\partial W_{11}^{(3)}} \\\\\] \[\text{From proof for $\frac{\partial}{\partial W^{(1)}_{11}}E$:}\] \[\frac{\partial E}{\partial a_1^{(4)}}=\frac{a_1^{(4)}-y}{a_1^{(4)}(1-a_1^{(4)})} \\\\\] \[\frac{\partial a_1^{(4)}}{\partial z_1^{(4)}} = a_1^{(4)}(1-a_1^{(4)}) \\\\\] \[\begin{align} \frac{\partial z_1^{(4)}}{\partial W_{11}^{(3)}} &= \frac{\partial }{\partial W_{11}^{(3)}}(W_{11}^{(3)}a_1^{(3)} + W_{21}^{(3)}a_2^{(3)} + W_{31}^{(3)}a_3^{(3)}) \\ &= \frac{\partial }{\partial W_{11}^{(3)}}(W_{11}^{(3)}a_1^{(3)}) + 0 + 0 \\ &= a_1^{(3)} \\\\ \end{align}\] \[\frac{\partial E}{\partial W_{11}^{(3)}} = \left(\frac{a_1^{(4)}-y}{a_1^{(4)}(1-a_1^{(4)})}\right) \cdot \left(a_1^{(4)}(1-a_1^{(4)})\right) \cdot \left( a_1^{(3)}\right) \ \ \ \ \blacksquare\\\\\]

Backprop Algorithm Pseudo-Code

for simplicity, bias units and regularization are left out

Bike Sharing Dataset With Implemented Pseudo-Code

Hyperparameters

• \(M=\) number of training examples
• \(m=\) batch size (assuming \(M\) divisible by \(m\))
• \(E=\) number of epochs to train for
• \(L=\) number of NN layers
• \(n=\) number of features per train sample
• \(c=\) number of classes
• \(\alpha=\) learning rate
• \([s_1,s_2,\ldots,s_l,\ldots,s_L] =\) number of neurons per layer list

Notation (Pythonic)

• same notation as NN Notation
• np.dot() : numpy dot product of vectors
• np.ndarray.T : numpy matrix transpose
• * : numpy element-wise multiplication
• np.ndarray.shape : numpy array shape
• sigmoid() : sigmoid function

Training Data (Pythonic)

• All training samples: \(X, Y\) numpy array
• Each training sample has features: \(X[i]=[[x_1,x_2,\ldots,x_n]]\)
• Each training sample has labels: \(Y[i]=[[y_1,y_2,\ldots,y_c]]\)

Object Attributes (Pythonic)

• Let \(len(W)=L\)
• for \(l\) in \(range(1,(L-1)+1)\)
  • Let \(W[l].shape=(s_{l+1},s_l)\)
    • Implies \(W[l][j].shape=(s_l,)\)
    • Implies \(W[l][j]=\text{vector of length}\ s_l\)
  • Let \(grad\_sum\_W[l].shape=(s_{l+1},s_l)\)
• Let \(X.shape=(M,n)=(M,s_1)\)
  • Implies \(X[i].shape=(s_1,)\)
  • Implies \(X[i]=\text{vector of length}\ s_1\)
• Let \(Y.shape=(M,c)=(M,s_L)\)
  • Implies \(Y[i].shape=(s_L,)\)
  • Implies \(Y[i]=\text{vector of length}\ s_L\)
• for \(l\) in \(range(1,L+1)\):
  • Let \(a[l].shape=(s_l,1)\)
  • Let \(\delta[l].shape=(s_l,1)\)

Pseudo-Code (Pythonic)

• for \(l\) in \(range(1,(L-1)+1)\)
  • Let \(grad\_sum\_W[l]=0\)
• for \(e\) in \(range(1,E+1)\):
  • for \(M_i, (x,y)\) in \(enumerate(zip(X,Y))\):
    • Let \(a[1]=x[:,None]\)
    • for \(l\) in \(range(2,L+1)\):
      • Compute \(a[l]=sigmoid(np.matmul(W[l-1],a[l-1]))\)
    • Compute \(\delta[L]=a[L]-y[:,None]\)
    • for \(l\) in \(range(2,(L-1)+1)\):
      • Compute \(\delta[l]=np.matmul(W[l].T,\delta[l+1])*a[l]*(1-a[l])\)
    • for \(l\) in \(range(1,(L-1)+1)\)
      • Update \(grad\_sum\_W[l]+=np.matmul(\delta[l+1],a[l].T)\)
    • if \((M_i+1)\ \%\ m == 0\):
      • for \(l\) in \(range(1,(L-1)+1)\)
        • Compute \(W[l]=W[l]-\alpha*\frac{1}{m}*grad\_sum\_W[l]\)
        • Let \(grad\_sum\_W[l]=0\)

Notation (Mathematical)

• same notation as NN Notation
• \(A^{T}\) : matrix transpose
• \(AB\) : matrix multiplication of matrices \(A\) and \(B\)
• \(A \circ B\) : element wise multiplication of matrices \(A\) and \(B\)
• \(\sigma()\) : sigmoid function

Training Data (Mathematical)

• All training samples: \((X_1,Y_1),(X_2,Y_2),\ldots,(X_M,Y_M)\)
• Each training sample has features: \((x_1,x_2,\ldots,x_n)\)
• Each training sample has labels: \((y_1,y_2,\ldots,y_n)\)

Matrix Visualizations (Mathematical)

\[\begin{align} W^{(l)} &= \begin{bmatrix} W^{(l)}_{11} & W^{(l)}_{21} & W^{(l)}_{31} & \ldots & W^{(l)}_{s_l1} \\ W^{(l)}_{12} & W^{(l)}_{22} & W^{(l)}_{32} \\ W^{(l)}_{13} & W^{(l)}_{23} & W^{(l)}_{33} \\ \vdots & & &\ddots \\ W^{(l)}_{1s_{l+1}} & & & & W^{(l)}_{s_ls_{l+1}} \\ \end{bmatrix} \\\\ X_i &= \begin{bmatrix} x_1 & x_2 & x_3 & \ldots & x_n \end{bmatrix} \\\\ Y_i &= \begin{bmatrix} y_1 & y_2 & y_3 & \ldots & y_c \end{bmatrix} \\\\ a^{(l)} &= \begin{bmatrix} a^{(l)}_1 \\ a^{(l)}_2 \\ a^{(l)}_3 \\ \ldots \\ a^{(l)}_{s_{l}} \end{bmatrix} \\\\ \delta^{(l)} &= \begin{bmatrix} \delta^{(l)}_1 \\ \delta^{(l)}_2 \\ \delta^{(l)}_3 \\ \ldots \\ \delta^{(l)}_{s_{l}} \end{bmatrix} \\\\ \frac{\partial}{\partial W^{(l)}}E &= \begin{bmatrix} \frac{\partial}{\partial W^{(l)}_{11}}E & \frac{\partial}{\partial W^{(l)}_{21}}E & \frac{\partial}{\partial W^{(l)}_{31}}E & \ldots & \frac{\partial}{\partial W^{(l)}_{s_l1}}E \\ \frac{\partial}{\partial W^{(l)}_{12}}E & \frac{\partial}{\partial W^{(l)}_{22}}E & \frac{\partial}{\partial W^{(l)}_{32}}E \\ \frac{\partial}{\partial W^{(l)}_{13}}E & \frac{\partial}{\partial W^{(l)}_{23}}E & \frac{\partial}{\partial W^{(l)}_{33}}E \\ \vdots & & &\ddots \\ \frac{\partial}{\partial W^{(l)}_{1s_{l+1}}}E & & & & \frac{\partial}{\partial W^{(l)}_{s_ls_{l+1}}}E \\ \end{bmatrix} \\\\ \end{align}\]

Pseudo-Code (Mathematical)

• \(\forall\ l\in\{1,\ldots,L-1\}\),
  • Let \(\frac{\partial}{\partial W^{(l)}}E = 0\)
• For every epoch:
  • For every train sample \((X_i,Y_i)\) in \((X_1,Y_1),\ldots,(X_M,Y_M)\):
    • Let \(a_1^{(1)}=x_1,\ a_2^{(1)}=x_2,\ \ldots,\ a_{s_1}^{(1)}=x_n\)
    • \(\forall\ l\in\{2,\ldots,L\}\),
      • Compute \(a^{(l)}=\sigma(W^{(l-1)}a^{(l-1)})\)
    • Compute \(\delta^{(L)}=a^{(L)}-Y_i^T\)
    • \(\forall\ l\in\{2,\ldots,L-1\}\),
      • Compute \(\delta^{(l)} = W^{(l)T}\delta^{(l+1)} \circ a^{(l)} \circ (1-a^{(l)})\)
    • \(\forall\ l\in\{1,\ldots,L-1\}\),
      • Update \(\frac{\partial}{\partial W^{(l)}}E = \frac{\partial}{\partial W^{(l)}}E+\delta^{(l+1)}a^{(l)T}\)
    • If computed gradients for \(m\) training samples:
      • \(\forall\ l\in\{1,\ldots,L-1\}\),
        • Update \(W^{(l)}\leftarrow W^{(l)}-\alpha\circ\frac{1}{m}\circ\frac{\partial}{\partial W^{(l)}}E\)
        • Let \(\frac{\partial}{\partial W^{(l)}}E = 0\)

“Proof”.

\[\text{WWTP: all matrix multiplications make sense} \\ \text{Take pythonic expression, "plug" in the shapes: }\] \[\begin{align} a[l] &= sigmoid(np.matmul(W[l-1],a[l-1])) \\ (s_l,1) &= sigmoid(np.matmul((s_l,s_{l-1}),(s_{l-1},1))) \\ (s_l,1) &= sigmoid((s_l,1)) \\ (s_l,1) &= (s_l,1) \ \ \ \ \blacksquare\\\\ \end{align}\] \[\begin{align} \delta[l] &= np.matmul(W[l].T,\delta[l+1])*a[l]*(1-a[l]) \\ (s_l,1) &= np.matmul((s_{l+1},s_l).T,(s_{l+1},1))*(s_l,1)*(1-(s_l,1)) \\ (s_l,1) &= np.matmul((s_l,s_{l+1}),(s_{l+1},1))*(s_l,1)*(1-(s_l,1)) \\ (s_l,1) &= (s_l,1)*(s_l,1)*(1-(s_l,1)) \\ (s_l,1) &= (s_l,1)*(s_l,1)*(s_l,1) \\ (s_l,1) &= (s_l,1) \ \ \ \ \blacksquare\\\\ \end{align}\] \[\begin{align} grad\_sum\_W[l] &+= np.matmul(\delta[l+1],a[l].T) \\ (s_{l+1},s_l) &+= np.matmul((s_{l+1},1),(s_l,1).T) \\ (s_{l+1},s_l) &+= np.matmul((s_{l+1},1),(1,s_l)) \\ (s_{l+1},s_l) &+= (s_{l+1},s_l) \ \ \ \ \blacksquare\\\\ \end{align}\]

“Proof”.

\[\text{WWTP: pseudo-code calculates partial derivatives correctly} \\ \text{Informal proof, } \\ \text{use pseudo-code to calculate partial derivatives for sample NN,} \\ \text{check results match with raw calculations.}\\\\\] \[\text{WWTP: Pseudo-Code yields}\] \[\begin{align} \frac{\partial}{\partial W^{(1)}_{11}}E &= \left(\frac{a_1^{(4)}-y}{a_1^{(4)}(1-a_1^{(4)})}\right) \\ &\phantom{0000} \cdot \left(a_1^{(4)}(1-a_1^{(4)})\right) \\ &\phantom{0000} \cdot \left(\left(W_{11}^{(3)} \cdot a_1^{(3)}(1-a_1^{(3)}) \cdot W_{11}^{(2)}\right) + \left(W_{21}^{(3)} \cdot a_2^{(3)}(1-a_2^{(3)}) \cdot W_{12}^{(2)}\right) + \left(W_{31}^{(3)} \cdot a_3^{(3)}(1-a_3^{(3)}) \cdot W_{13}^{(2)}\right)\right) \\ &\phantom{0000} \cdot \left(a_1^{(2)}(1-a_1^{(2)})\right) \\ &\phantom{0000} \cdot \left(a_1^{(1)}\right) \end{align}\] \[\begin{align} \frac{\partial}{\partial W^{(1)}_{21}}E &= \left(\frac{a_1^{(4)}-y}{a_1^{(4)}(1-a_1^{(4)})}\right) \\ &\phantom{0000} \cdot \left(a_1^{(4)}(1-a_1^{(4)})\right) \\ &\phantom{0000} \cdot \left(\left(W_{11}^{(3)} \cdot a_1^{(3)}(1-a_1^{(3)}) \cdot W_{11}^{(2)}\right) + \left(W_{21}^{(3)} \cdot a_2^{(3)}(1-a_2^{(3)}) \cdot W_{12}^{(2)}\right) + \left(W_{31}^{(3)} \cdot a_3^{(3)}(1-a_3^{(3)}) \cdot W_{13}^{(2)}\right)\right) \\ &\phantom{0000} \cdot \left(a_1^{(2)}(1-a_1^{(2)})\right) \\ &\phantom{0000} \cdot \left(a_2^{(1)}\right) \end{align}\] \[\begin{align} \frac{\partial}{\partial W^{(3)}_{11}}E &= \left(\frac{a_1^{(4)}-y}{a_1^{(4)}(1-a_1^{(4)})}\right) \cdot \left(a_1^{(4)}(1-a_1^{(4)})\right) \cdot \left( a_1^{(3)}\right) \\\\ &=(a_1^{(4)}-y)a_1^{(3)} \\\\ \end{align}\] \[\text{Executing Pseudo-Code (Mathematical):} \\ \text{Forward Propagation, calculating activations:}\] \[\begin{align} a^{(1)} &= \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} \\\\ a^{(2)} &= \sigma(W^{(1)}a^{(1)}) \\ &=\sigma\left( \begin{bmatrix} W^{(1)}_{11} & W^{(1)}_{21} & W^{(1)}_{31} \\ W^{(1)}_{12} & W^{(1)}_{22} & W^{(1)}_{32} \\ W^{(1)}_{13} & W^{(1)}_{23} & W^{(1)}_{33} \\ W^{(1)}_{14} & W^{(1)}_{24} & W^{(1)}_{34} \\ \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} \right) \\ &=\sigma\left( \begin{bmatrix} W^{(1)}_{11}x_1 + W^{(1)}_{21}x_2 + W^{(1)}_{31}x_3 \\ W^{(1)}_{12}x_1 + W^{(1)}_{22}x_2 + W^{(1)}_{32}x_3 \\ W^{(1)}_{13}x_1 + W^{(1)}_{23}x_2 + W^{(1)}_{33}x_3 \\ W^{(1)}_{14}x_1 + W^{(1)}_{24}x_2 + W^{(1)}_{34}x_3 \\ \end{bmatrix} \right) \\ &=\begin{bmatrix} \sigma\left(W^{(1)}_{11}x_1 + W^{(1)}_{21}x_2 + W^{(1)}_{31}x_3\right) \\ \sigma\left(W^{(1)}_{12}x_1 + W^{(1)}_{22}x_2 + W^{(1)}_{32}x_3\right) \\ \sigma\left(W^{(1)}_{13}x_1 + W^{(1)}_{23}x_2 + W^{(1)}_{33}x_3\right) \\ \sigma\left(W^{(1)}_{14}x_1 + W^{(1)}_{24}x_2 + W^{(1)}_{34}x_3\right) \\ \end{bmatrix} \\\\ a^{(3)} &= \sigma(W^{(2)}a^{(2)}) \\ &=\sigma\left( \begin{bmatrix} W^{(2)}_{11} & W^{(2)}_{21} & W^{(2)}_{31} & W^{(2)}_{41} \\ W^{(2)}_{12} & W^{(2)}_{22} & W^{(2)}_{32} & W^{(2)}_{42} \\ W^{(2)}_{13} & W^{(2)}_{23} & W^{(2)}_{33} & W^{(2)}_{43} \\ \end{bmatrix} \begin{bmatrix} a^{(2)}_1 \\ a^{(2)}_2 \\ a^{(2)}_3 \\ a^{(2)}_4 \end{bmatrix} \right) \\ &=\sigma\left( \begin{bmatrix} W^{(2)}_{11}a^{(2)}_1 + W^{(2)}_{21}a^{(2)}_2 + W^{(2)}_{31}a^{(2)}_3 + W^{(2)}_{41}a^{(2)}_4 \\ W^{(2)}_{12}a^{(2)}_1 + W^{(2)}_{22}a^{(2)}_2 + W^{(2)}_{32}a^{(2)}_3 + W^{(2)}_{42}a^{(2)}_4 \\ W^{(2)}_{13}a^{(2)}_1 + W^{(2)}_{23}a^{(2)}_2 + W^{(2)}_{33}a^{(2)}_3 + W^{(2)}_{43}a^{(2)}_4 \\ \end{bmatrix} \right) \\ &=\begin{bmatrix} \sigma\left(W^{(2)}_{11}a^{(2)}_1 + W^{(2)}_{21}a^{(2)}_2 + W^{(2)}_{31}a^{(2)}_3 + W^{(2)}_{41}a^{(2)}_4\right) \\ \sigma\left(W^{(2)}_{12}a^{(2)}_1 + W^{(2)}_{22}a^{(2)}_2 + W^{(2)}_{32}a^{(2)}_3 + W^{(2)}_{42}a^{(2)}_4\right) \\ \sigma\left(W^{(2)}_{13}a^{(2)}_1 + W^{(2)}_{23}a^{(2)}_2 + W^{(2)}_{33}a^{(2)}_3 + W^{(2)}_{43}a^{(2)}_4\right) \\ \end{bmatrix} \\\\ a^{(4)} &= \sigma(W^{(3)}a^{(3)}) \\ &=\sigma\left( \begin{bmatrix} W^{(3)}_{11} & W^{(3)}_{21} & W^{(3)}_{31} \\ \end{bmatrix} \begin{bmatrix} a^{(3)}_1 \\ a^{(3)}_2 \\ a^{(3)}_3 \end{bmatrix} \right) \\ &=\sigma\left( \begin{bmatrix} W^{(3)}_{11}a^{(3)}_1 + W^{(3)}_{21}a^{(3)}_2 + W^{(3)}_{31}a^{(3)}_3 \\ \end{bmatrix} \right) \\ &=\begin{bmatrix} \sigma\left(W^{(3)}_{11}a^{(3)}_1 + W^{(3)}_{21}a^{(3)}_2 + W^{(3)}_{31}a^{(3)}_3\right) \\ \end{bmatrix} \\\\ \end{align}\] \[\text{Backpropagation, calculating errors:}\] \[\begin{align} \delta^{(4)} &= a^{(4)}-Y_i^T \\ &= \begin{bmatrix} \sigma\left(W^{(3)}_{11}a^{(3)}_1 + W^{(3)}_{21}a^{(3)}_2 + W^{(3)}_{31}a^{(3)}_3\right) \\ \end{bmatrix} -\begin{bmatrix}y_1\end{bmatrix}^T \\ &= \begin{bmatrix} \sigma\left(W^{(3)}_{11}a^{(3)}_1 + W^{(3)}_{21}a^{(3)}_2 + W^{(3)}_{31}a^{(3)}_3\right) \\ \end{bmatrix} -\begin{bmatrix}y_1\end{bmatrix} \\ &= \begin{bmatrix} a^{(4)}_1 - y_1 \\ \end{bmatrix}\\\\ &\text{For simplicity and consistency, Let $y=y_1$:} \\ \delta^{(4)} &= a^{(4)}_1 - y \\\\ \delta^{(3)} &= W^{(3)T}\delta^{(4)} \circ a^{(3)} \circ (1-a^{(3)}) \\ &= \begin{bmatrix} W^{(3)}_{11} & W^{(3)}_{21} & W^{(3)}_{31} \\ \end{bmatrix}^T \begin{bmatrix} a^{(4)}_1 - y \\ \end{bmatrix} \circ a^{(3)} \circ (1-a^{(3)}) \\ &= \begin{bmatrix} W^{(3)}_{11} \\ W^{(3)}_{21} \\ W^{(3)}_{31} \\ \end{bmatrix} \begin{bmatrix} a^{(4)}_1 - y \\ \end{bmatrix} \circ a^{(3)} \circ (1-a^{(3)}) \\ &= \begin{bmatrix} W^{(3)}_{11}(a^{(4)}_1 - y) \\ W^{(3)}_{21}(a^{(4)}_1 - y) \\ W^{(3)}_{31}(a^{(4)}_1 - y) \\ \end{bmatrix} \circ a^{(3)} \circ (1-a^{(3)}) \\ &= \begin{bmatrix} W^{(3)}_{11}(a^{(4)}_1 - y) \\ W^{(3)}_{21}(a^{(4)}_1 - y) \\ W^{(3)}_{31}(a^{(4)}_1 - y) \\ \end{bmatrix} \circ \begin{bmatrix}a^{(3)}_1 \\ a^{(3)}_2 \\ a^{(3)}_3 \end{bmatrix} \circ (1 - \begin{bmatrix}a^{(3)}_1 \\ a^{(3)}_2 \\ a^{(3)}_3 \end{bmatrix}) \\ &= \begin{bmatrix} W^{(3)}_{11}(a^{(4)}_1 - y) \\ W^{(3)}_{21}(a^{(4)}_1 - y) \\ W^{(3)}_{31}(a^{(4)}_1 - y) \\ \end{bmatrix} \circ \begin{bmatrix}a^{(3)}_1 \\ a^{(3)}_2 \\ a^{(3)}_3 \end{bmatrix} \circ \begin{bmatrix}1 - a^{(3)}_1 \\ 1 - a^{(3)}_2 \\ 1 - a^{(3)}_3 \end{bmatrix} \\ &= \begin{bmatrix} W^{(3)}_{11}(a^{(4)}_1 - y)a^{(3)}_1(1 - a^{(3)}_1) \\ W^{(3)}_{21}(a^{(4)}_1 - y)a^{(3)}_2(1 - a^{(3)}_2) \\ W^{(3)}_{31}(a^{(4)}_1 - y)a^{(3)}_3(1 - a^{(3)}_3) \\ \end{bmatrix}\\\\ \end{align}\] \[\begin{align} \delta^{(2)} &= W^{(2)T}\delta^{(3)} \circ a^{(2)} \circ (1-a^{(2)}) \\ &= \begin{bmatrix} W^{(2)}_{11} & W^{(2)}_{21} & W^{(2)}_{31} & W^{(2)}_{41} \\ W^{(2)}_{12} & W^{(2)}_{22} & W^{(2)}_{32} & W^{(2)}_{42} \\ W^{(2)}_{13} & W^{(2)}_{23} & W^{(2)}_{33} & W^{(2)}_{43} \\ \end{bmatrix}^T \begin{bmatrix} W^{(3)}_{11}(a^{(4)}_1 - y)a^{(3)}_1(1 - a^{(3)}_1) \\ W^{(3)}_{21}(a^{(4)}_1 - y)a^{(3)}_2(1 - a^{(3)}_2) \\ W^{(3)}_{31}(a^{(4)}_1 - y)a^{(3)}_3(1 - a^{(3)}_3) \\ \end{bmatrix} \circ a^{(2)} \circ (1-a^{(2)}) \\ &= \begin{bmatrix} W^{(2)}_{11} & W^{(2)}_{12} & W^{(2)}_{13} \\ W^{(2)}_{21} & W^{(2)}_{22} & W^{(2)}_{23} \\ W^{(2)}_{31} & W^{(2)}_{32} & W^{(2)}_{33} \\ W^{(2)}_{41} & W^{(2)}_{42} & W^{(2)}_{43} \\ \end{bmatrix} \begin{bmatrix} W^{(3)}_{11}(a^{(4)}_1 - y)a^{(3)}_1(1 - a^{(3)}_1) \\ W^{(3)}_{21}(a^{(4)}_1 - y)a^{(3)}_2(1 - a^{(3)}_2) \\ W^{(3)}_{31}(a^{(4)}_1 - y)a^{(3)}_3(1 - a^{(3)}_3) \\ \end{bmatrix} \circ a^{(2)} \circ (1-a^{(2)}) \\ &= \begin{bmatrix} \left(\left(W^{(3)}_{11}(a^{(4)}_1 - y)a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{11}\right) + \left(W^{(3)}_{21}(a^{(4)}_1 - y)a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{12}\right) + \left(W^{(3)}_{31}(a^{(4)}_1 - y)a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{13}\right)\right) \\ \left(\left(W^{(3)}_{11}(a^{(4)}_1 - y)a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{21}\right) + \left(W^{(3)}_{21}(a^{(4)}_1 - y)a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{22}\right) + \left(W^{(3)}_{31}(a^{(4)}_1 - y)a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{23}\right)\right) \\ \left(\left(W^{(3)}_{11}(a^{(4)}_1 - y)a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{31}\right) + \left(W^{(3)}_{21}(a^{(4)}_1 - y)a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{32}\right) + \left(W^{(3)}_{31}(a^{(4)}_1 - y)a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{33}\right)\right) \\ \left(\left(W^{(3)}_{11}(a^{(4)}_1 - y)a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{41}\right) + \left(W^{(3)}_{21}(a^{(4)}_1 - y)a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{42}\right) + \left(W^{(3)}_{31}(a^{(4)}_1 - y)a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{43}\right)\right) \\ \end{bmatrix} \circ a^{(2)} \circ (1-a^{(2)}) \\\\ &= \begin{bmatrix} (a^{(4)}_1 - y)\left(\left(W^{(3)}_{11}a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{11}\right) + \left(W^{(3)}_{21}a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{12}\right) + \left(W^{(3)}_{31}a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{13}\right)\right) \\ (a^{(4)}_1 - y)\left(\left(W^{(3)}_{11}a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{21}\right) + \left(W^{(3)}_{21}a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{22}\right) + \left(W^{(3)}_{31}a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{23}\right)\right) \\ (a^{(4)}_1 - y)\left(\left(W^{(3)}_{11}a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{31}\right) + \left(W^{(3)}_{21}a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{32}\right) + \left(W^{(3)}_{31}a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{33}\right)\right) \\ (a^{(4)}_1 - y)\left(\left(W^{(3)}_{11}a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{41}\right) + \left(W^{(3)}_{21}a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{42}\right) + \left(W^{(3)}_{31}a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{43}\right)\right) \\ \end{bmatrix} \circ a^{(2)} \circ (1-a^{(2)}) \\\\ &= \begin{bmatrix} (a^{(4)}_1 - y)\left(\left(W^{(3)}_{11}a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{11}\right) + \left(W^{(3)}_{21}a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{12}\right) + \left(W^{(3)}_{31}a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{13}\right)\right) \\ (a^{(4)}_1 - y)\left(\left(W^{(3)}_{11}a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{21}\right) + \left(W^{(3)}_{21}a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{22}\right) + \left(W^{(3)}_{31}a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{23}\right)\right) \\ (a^{(4)}_1 - y)\left(\left(W^{(3)}_{11}a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{31}\right) + \left(W^{(3)}_{21}a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{32}\right) + \left(W^{(3)}_{31}a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{33}\right)\right) \\ (a^{(4)}_1 - y)\left(\left(W^{(3)}_{11}a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{41}\right) + \left(W^{(3)}_{21}a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{42}\right) + \left(W^{(3)}_{31}a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{43}\right)\right) \\ \end{bmatrix} \circ \begin{bmatrix}a^{(2)}_1 \\ a^{(2)}_2 \\ a^{(2)}_3 \\ a^{(2)}_4\end{bmatrix} \circ (1-\begin{bmatrix}a^{(2)}_1 \\ a^{(2)}_2 \\ a^{(2)}_3 \\ a^{(2)}_4\end{bmatrix}) \\\\ &= \begin{bmatrix} (a^{(4)}_1 - y)\left(\left(W^{(3)}_{11}a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{11}\right) + \left(W^{(3)}_{21}a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{12}\right) + \left(W^{(3)}_{31}a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{13}\right)\right)a^{(2)}_1(1-a^{(2)}_1) \\ (a^{(4)}_1 - y)\left(\left(W^{(3)}_{11}a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{21}\right) + \left(W^{(3)}_{21}a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{22}\right) + \left(W^{(3)}_{31}a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{23}\right)\right)a^{(2)}_2(1-a^{(2)}_2) \\ (a^{(4)}_1 - y)\left(\left(W^{(3)}_{11}a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{31}\right) + \left(W^{(3)}_{21}a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{32}\right) + \left(W^{(3)}_{31}a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{33}\right)\right)a^{(2)}_3(1-a^{(2)}_3) \\ (a^{(4)}_1 - y)\left(\left(W^{(3)}_{11}a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{41}\right) + \left(W^{(3)}_{21}a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{42}\right) + \left(W^{(3)}_{31}a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{43}\right)\right)a^{(2)}_4(1-a^{(2)}_4) \\ \end{bmatrix} \\\\ \end{align}\] \[\text{Calculating partial derivatives using errors:}\] \[\begin{align} \frac{\partial}{\partial W^{(3)}}E &= \delta^{(4)}a^{(3)T} \\ &= \begin{bmatrix}a^{(4)}_1 - y \end{bmatrix}\begin{bmatrix}a^{(3)}_1 \\ a^{(3)}_2 \\ a^{(3)}_3\end{bmatrix}^T \\ &= \begin{bmatrix}a^{(4)}_1 - y \end{bmatrix}\begin{bmatrix}a^{(3)}_1 & a^{(3)}_2 & a^{(3)}_3\end{bmatrix} \\ &= \begin{bmatrix}(a^{(4)}_1 - y)a^{(3)}_1 & (a^{(4)}_1 - y)a^{(3)}_2 & (a^{(4)}_1 - y)a^{(3)}_3\end{bmatrix} \\ \end{align}\] \[\begin{align} \frac{\partial}{\partial W^{(2)}}E &= \delta^{(3)}a^{(2)T} \\ &= \begin{bmatrix} W^{(3)}_{11}(a^{(4)}_1 - y)a^{(3)}_1(1 - a^{(3)}_1) \\ W^{(3)}_{21}(a^{(4)}_1 - y)a^{(3)}_2(1 - a^{(3)}_2) \\ W^{(3)}_{31}(a^{(4)}_1 - y)a^{(3)}_3(1 - a^{(3)}_3) \\ \end{bmatrix} \begin{bmatrix} a^{(2)}_1 \\ a^{(2)}_2 \\ a^{(2)}_3 \\ a^{(2)}_4 \end{bmatrix}^T \\ &= \begin{bmatrix} W^{(3)}_{11}(a^{(4)}_1 - y)a^{(3)}_1(1 - a^{(3)}_1) \\ W^{(3)}_{21}(a^{(4)}_1 - y)a^{(3)}_2(1 - a^{(3)}_2) \\ W^{(3)}_{31}(a^{(4)}_1 - y)a^{(3)}_3(1 - a^{(3)}_3) \\ \end{bmatrix} \begin{bmatrix} a^{(2)}_1 & a^{(2)}_2 & a^{(2)}_3 & a^{(2)}_4 \end{bmatrix} \\ &= \begin{bmatrix} \left(W^{(3)}_{11}(a^{(4)}_1 - y)a^{(3)}_1(1 - a^{(3)}_1)a^{(2)}_1\right) & \left(W^{(3)}_{11}(a^{(4)}_1 - y)a^{(3)}_1(1 - a^{(3)}_1)a^{(2)}_2\right) & \left(W^{(3)}_{11}(a^{(4)}_1 - y)a^{(3)}_1(1 - a^{(3)}_1)a^{(2)}_3\right) & \left(W^{(3)}_{11}(a^{(4)}_1 - y)a^{(3)}_1(1 - a^{(3)}_1)a^{(2)}_4\right) \\ \left(W^{(3)}_{21}(a^{(4)}_1 - y)a^{(3)}_2(1 - a^{(3)}_2)a^{(2)}_1\right) & \left(W^{(3)}_{21}(a^{(4)}_1 - y)a^{(3)}_2(1 - a^{(3)}_2)a^{(2)}_2\right) & \left(W^{(3)}_{21}(a^{(4)}_1 - y)a^{(3)}_2(1 - a^{(3)}_2)a^{(2)}_3\right) & \left(W^{(3)}_{21}(a^{(4)}_1 - y)a^{(3)}_2(1 - a^{(3)}_2)a^{(2)}_4\right) \\ \left(W^{(3)}_{31}(a^{(4)}_1 - y)a^{(3)}_3(1 - a^{(3)}_3)a^{(2)}_1\right) & \left(W^{(3)}_{31}(a^{(4)}_1 - y)a^{(3)}_3(1 - a^{(3)}_3)a^{(2)}_2\right) & \left(W^{(3)}_{31}(a^{(4)}_1 - y)a^{(3)}_3(1 - a^{(3)}_3)a^{(2)}_3\right) & \left(W^{(3)}_{31}(a^{(4)}_1 - y)a^{(3)}_3(1 - a^{(3)}_3)a^{(2)}_4\right) \\ \end{bmatrix} \end{align}\] \[\begin{align} \frac{\partial}{\partial W^{(1)}}E &= \delta^{(2)}a^{(1)T} \\ &=\begin{bmatrix} (a^{(4)}_1 - y)\left(\left(W^{(3)}_{11}a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{11}\right) + \left(W^{(3)}_{21}a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{12}\right) + \left(W^{(3)}_{31}a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{13}\right)\right)a^{(2)}_1(1-a^{(2)}_1) \\ (a^{(4)}_1 - y)\left(\left(W^{(3)}_{11}a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{21}\right) + \left(W^{(3)}_{21}a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{22}\right) + \left(W^{(3)}_{31}a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{23}\right)\right)a^{(2)}_2(1-a^{(2)}_2) \\ (a^{(4)}_1 - y)\left(\left(W^{(3)}_{11}a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{31}\right) + \left(W^{(3)}_{21}a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{32}\right) + \left(W^{(3)}_{31}a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{33}\right)\right)a^{(2)}_3(1-a^{(2)}_3) \\ (a^{(4)}_1 - y)\left(\left(W^{(3)}_{11}a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{41}\right) + \left(W^{(3)}_{21}a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{42}\right) + \left(W^{(3)}_{31}a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{43}\right)\right)a^{(2)}_4(1-a^{(2)}_4) \\ \end{bmatrix} \begin{bmatrix}a^{(1)}_1 \\ a^{(1)}_2 \\ a^{(1)}_3\end{bmatrix}^T \\ &=\begin{bmatrix} (a^{(4)}_1 - y)\left(\left(W^{(3)}_{11}a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{11}\right) + \left(W^{(3)}_{21}a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{12}\right) + \left(W^{(3)}_{31}a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{13}\right)\right)a^{(2)}_1(1-a^{(2)}_1) \\ (a^{(4)}_1 - y)\left(\left(W^{(3)}_{11}a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{21}\right) + \left(W^{(3)}_{21}a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{22}\right) + \left(W^{(3)}_{31}a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{23}\right)\right)a^{(2)}_2(1-a^{(2)}_2) \\ (a^{(4)}_1 - y)\left(\left(W^{(3)}_{11}a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{31}\right) + \left(W^{(3)}_{21}a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{32}\right) + \left(W^{(3)}_{31}a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{33}\right)\right)a^{(2)}_3(1-a^{(2)}_3) \\ (a^{(4)}_1 - y)\left(\left(W^{(3)}_{11}a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{41}\right) + \left(W^{(3)}_{21}a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{42}\right) + \left(W^{(3)}_{31}a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{43}\right)\right)a^{(2)}_4(1-a^{(2)}_4) \\ \end{bmatrix} \begin{bmatrix}a^{(1)}_1 & a^{(1)}_2 & a^{(1)}_3\end{bmatrix} \\ &=\begin{bmatrix} \left((a^{(4)}_1 - y)\left(\left(W^{(3)}_{11}a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{11}\right) + \left(W^{(3)}_{21}a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{12}\right) + \left(W^{(3)}_{31}a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{13}\right)\right)a^{(2)}_1(1-a^{(2)}_1)a^{(1)}_1\right) & \left((a^{(4)}_1 - y)\left(\left(W^{(3)}_{11}a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{11}\right) + \left(W^{(3)}_{21}a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{12}\right) + \left(W^{(3)}_{31}a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{13}\right)\right)a^{(2)}_1(1-a^{(2)}_1)a^{(1)}_2\right) & \left((a^{(4)}_1 - y)\left(\left(W^{(3)}_{11}a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{11}\right) + \left(W^{(3)}_{21}a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{12}\right) + \left(W^{(3)}_{31}a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{13}\right)\right)a^{(2)}_1(1-a^{(2)}_1)a^{(1)}_3\right) \\ \left((a^{(4)}_1 - y)\left(\left(W^{(3)}_{11}a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{21}\right) + \left(W^{(3)}_{21}a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{22}\right) + \left(W^{(3)}_{31}a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{23}\right)\right)a^{(2)}_2(1-a^{(2)}_2)a^{(1)}_1\right) & \left((a^{(4)}_1 - y)\left(\left(W^{(3)}_{11}a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{21}\right) + \left(W^{(3)}_{21}a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{22}\right) + \left(W^{(3)}_{31}a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{23}\right)\right)a^{(2)}_2(1-a^{(2)}_2)a^{(1)}_2\right) & \left((a^{(4)}_1 - y)\left(\left(W^{(3)}_{11}a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{21}\right) + \left(W^{(3)}_{21}a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{22}\right) + \left(W^{(3)}_{31}a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{23}\right)\right)a^{(2)}_2(1-a^{(2)}_2)a^{(1)}_3\right) \\ \left((a^{(4)}_1 - y)\left(\left(W^{(3)}_{11}a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{31}\right) + \left(W^{(3)}_{21}a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{32}\right) + \left(W^{(3)}_{31}a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{33}\right)\right)a^{(2)}_3(1-a^{(2)}_3)a^{(1)}_1\right) & \left((a^{(4)}_1 - y)\left(\left(W^{(3)}_{11}a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{31}\right) + \left(W^{(3)}_{21}a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{32}\right) + \left(W^{(3)}_{31}a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{33}\right)\right)a^{(2)}_3(1-a^{(2)}_3)a^{(1)}_2\right) & \left((a^{(4)}_1 - y)\left(\left(W^{(3)}_{11}a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{31}\right) + \left(W^{(3)}_{21}a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{32}\right) + \left(W^{(3)}_{31}a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{33}\right)\right)a^{(2)}_3(1-a^{(2)}_3)a^{(1)}_3\right) \\ \left((a^{(4)}_1 - y)\left(\left(W^{(3)}_{11}a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{41}\right) + \left(W^{(3)}_{21}a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{42}\right) + \left(W^{(3)}_{31}a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{43}\right)\right)a^{(2)}_4(1-a^{(2)}_4)a^{(1)}_1\right) & \left((a^{(4)}_1 - y)\left(\left(W^{(3)}_{11}a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{41}\right) + \left(W^{(3)}_{21}a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{42}\right) + \left(W^{(3)}_{31}a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{43}\right)\right)a^{(2)}_4(1-a^{(2)}_4)a^{(1)}_2\right) & \left((a^{(4)}_1 - y)\left(\left(W^{(3)}_{11}a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{41}\right) + \left(W^{(3)}_{21}a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{42}\right) + \left(W^{(3)}_{31}a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{43}\right)\right)a^{(2)}_4(1-a^{(2)}_4)a^{(1)}_3\right) \\ \end{bmatrix} \\\\ \end{align}\] \[\text{According to calculations:}\] \[\begin{align} \frac{\partial}{\partial W^{(3)}_{11}}E &= (a^{(4)}_1 - y)a^{(3)}_1 \\ \frac{\partial}{\partial W^{(1)}_{11}}E &= (a^{(4)}_1 - y)\left(\left(W^{(3)}_{11}a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{11}\right) + \left(W^{(3)}_{21}a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{12}\right) + \left(W^{(3)}_{31}a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{13}\right)\right)a^{(2)}_1(1-a^{(2)}_1)a^{(1)}_1 \\ \frac{\partial}{\partial W^{(1)}_{21}}E &= (a^{(4)}_1 - y)\left(\left(W^{(3)}_{11}a^{(3)}_1(1 - a^{(3)}_1)W^{(2)}_{11}\right) + \left(W^{(3)}_{21}a^{(3)}_2(1 - a^{(3)}_2)W^{(2)}_{12}\right) + \left(W^{(3)}_{31}a^{(3)}_3(1 - a^{(3)}_3)W^{(2)}_{13}\right)\right)a^{(2)}_1(1-a^{(2)}_1)a^{(1)}_2 \\\\ \end{align}\] \[\text{Therefore the results from pseudo-code match raw calculations} \ \ \ \ \blacksquare\\\\\]

Backprop Clarifying Discrepancies

According to pseudo-code:

\[\text{error} = \text{pred} - \text{label}\] \[\begin{align} \text{weights } &-= \text{learnrate} * \text{partial derivative} \\ &-= \text{learnrate} * (\text{pred} - \text{label})\ldots \\ \end{align}\]

A variation that yields the same results (as seen in Udacity DL course):

\[\text{error} = \text{label} - \text{pred}\] \[\begin{align} \text{weights } &+= \text{learnrate} * \text{partial derivative} \\ &+= \text{learnrate} * (\text{label} - \text{pred})\ldots \\ \end{align}\]

Both versions of pseudo-code yield identical results.

“Proof”.

\[\text{In the end the pseudo-code's purpose,} \\ \text{is to calculate the partial derivative of error with respect to weights,} \\ \text{and this is done using the chain rule, for example:} \\\] \[\begin{align} \frac{\partial E}{\partial \hat{y}}&=\frac{\partial}{\partial \hat{y}}(-y\ln(\hat{y})-(1-y)\ln(1-\hat{y}))\\ &=\frac{\hat{y}-y}{\hat{y}(1-\hat{y})} \\\\ \end{align}\] \[\text{Therefore the following has to be true:} \\ \text{error} = \text{pred} - \text{label}\] \[\text{And to update the weights, we subtract the partial derivative from weight:}\] \[\begin{align} \text{weights } &-= \text{learnrate} * \text{partial derivative} \\ &-= \text{learnrate} * (\text{pred} - \text{label})\ldots \\\\ \end{align}\] \[\text{The previous steps validated the pseudo-code, but not the variation,} \\ \text{The variation is essentially the same, except the negative is "distributed":} \\\] \[\begin{align} \text{weights } &-= \text{learnrate} * \text{partial derivative} \\ &-= \text{learnrate} * (\text{pred} - \text{label})\ldots \\ &+= \text{learnrate} * -1(\text{pred} - \text{label})\ldots \\ &+= \text{learnrate} * (\text{label}-\text{pred})\ldots \\ &\implies \text{error} = \text{label}-\text{pred} \end{align}\] \[\text{And we find the variation yields the same results as the original.} \ \ \ \ \blacksquare\\\\\]

Discovering Backprop Formula From Scratch

1. Try manually computing single partial derivative (like before using the chain rule) for some sample neural network
2. Try computing multiple partial derivatives
3. Note the patterns, transform every part in chain rule into matrix multiplication to calculate all partial derivatives for a layer, for the sample NN
4. Generalize calculations to NN of any size
   • Notice how coming up with any algorithm requires: performing manually, then generalizing results

NN Toolkit

• Early stopping: choose model with lowest testing error, which indicates best generalization (result: model can avoid under and overfitting)
• Regularization: penalize larger weight values with higher error (result: prevent overfitting)
  • L1 Regularization:
    • \[E = -\frac{1}{m} \sum_{i=1}^m (1-y_i)\ln(1-\hat{y}_i) + y_i\ln(\hat{y}_i) + \lambda(|w_1|+\ldots+|w_n|)\]
    • why L1? End up with sparse vectors \(\implies\) small weights tend to go to 0 \(\implies\) reduction in number of weights (also \(\implies\) good for feature selection, as non-zero weight indicates important feature)
  • L2 Regularization:
    • \[E = -\frac{1}{m} \sum_{i=1}^m (1-y_i)\ln(1-\hat{y}_i) + y_i\ln(\hat{y}_i) + \lambda(w_1^2+\ldots+w_n^2)\]
    • why L2? Makes all weights equally small \(\implies\) doesn’t favor sparse vectors \(\implies\) better results for training models
    • why absolute value of L1 causes sparse vectors? it treats the weights \((1,0)\) and \((0.5,0.5)\) as equal errors of \(\|1\|+\|0\|=\|0.5\|+\|0.5\|=1\) whereas L2 treats \((1,0)=1^2+0^2=1\) as worse error compared to \((0.5,0.5)=0.5^2+0.5^2=0.5\)
• Dropout: set probability, probability designates whether neuron is dropped each epoch, the dropped neuron does not train causing other neurons to receive more training (result: reduces overfitting)
• Activation Functions:
  • tanh (hyperbolic tangent function): larger gradients, towards ends, compared to sigmoid \(tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}\)
  • ReLU (rectified linear unit): \(relu(x)=\begin{cases}x & \text{if $x\geq0$}.\\0 & \text{if $x<0$}.\end{cases}\)
• Batch gradient descent: computes the gradient using the whole dataset
• Stochastic gradient descent (SGD): computes the gradient using a single sample, or minibatch of samples (larger minibatch size allows you to avoid local minima)
• Random restart: train from different initializations of same model
• Momentum:
  • as you descend gradient, “gain momentum” and barrel through local minima to global minima
  • average most recent gradients to calculate “momentum”
  • with the more recent gradients having larger weights in a weighted average
  • \(\beta\) parameter : \(\text{step}(n) = \text{step}(n) + \beta\text{step}(n-1)+\beta^2\text{step}(n-2)+\ldots\)

Creating NN

• outline how you (as a human) would solve problem
• validate your assumptions through the data (never make any assumptions, about data, models, etc…, unless you can fully justify)
• build initial NN to capture signal (signal = useful info)
• debug and improve NN :
  • (do not focus on tune hyperparamters)
  • re-structure either data, or NN to make it easier for the NN to find right signals (the ones you use to solve the problem) and reduce noise
  • (literally like the sentiment NN, using your head, changing one “+” sign drastically increased results)
  • (goes to show you sometimes the key to winning is really using your mind, especially in kaggle competitions, the parameter tuning stuff you can learn how to do)
  • if (satisfied with accuracy) and (need faster):
    • simplify neural network to maintain same amount of signal, and reduce training time